
Computer Science C++ Lesson 22:
Merge and Mergesort
INTRODUCTION: In Lesson 20, we studied the quadratic sorting algorithms. We saw how the number of steps required increased as an N2 factor when sorting N elements. In the next two lessons we will study two recursive sorts, mergesort and quicksort, which work by dividing lists in half. In this lesson, after solving a preliminary merge problem, you will code a recursive mergesort.
The key topics for this lesson are:
A. A Merge Algorithm
B. A Non-Recursive Mergesort
C. Recursive Mergesort
D. Order of Recursive Mergesort
VOCABULARY: MERGE MERGESORT
DISCUSSION: A. A Merge Algorithm
1. The
mergesort algorithm requires a merge algorithm which we will solve first.
2. The
function prototype and the specifications of the merge routine are given below.
You may assume the array definitions from the sorting template program in
Lesson 19 apply, mainly that the number of data is stored in position 0 of the
array.
void
merge
(const apvector<int>&A,
const apvector<int>&B,
apvector<int> &C);
{Preconditions:
Lists A and B
are sorted in nondecreasing order.}
{Action:
Lists A and B
are merged into one list, C.}
{Postcondition:
List C contains all the values
from Lists A and B,}
{
in nondecreasing order.}
3. The merge function breaks down into four cases:
a. List A is done, so pull a value from List B.
b. List B is done, so pull a value from List A.
c. Neither is done, and if List A[i] < List B[j] (where i & j are index markers in lists A and B) then pull from List A.
d. Neither is done, and if List B[j] <= List A[i] then pull from List B.
4. It is important to deal with the four cases in the order described above. For example, if you are done with List A (if i > A[0]), you do not want to inspect any values past A[i].
B: 4
5 9
13 17 25
29
C: 2 4 5 6 9 11 13 15 17 21 25 29
B. A Non-Recursive Mergesort
1. The overall logic of mergesort is to "divide and conquer." A list of random integers will be split into two equal-sized lists (each with the same number of elements, plus or minus one), with each half-list sorted independently of the other. The next step will be to merge the two sorted sublists back into one sorted list.
2. Here is a non-recursive mergesort function:
void mergeSort (apvector<int> &A, int first, int last)
/* List A is unsorted, with A[0] values in the array.
first is the index position of the first value, last is the
index position of the last value in the array;
first < last.
{
int mid;
mid = (first + last) / 2;
selectionSort (A, first, mid);
selectionSort (A, mid+1, last);
merge (A, first, mid, last);
}
4. The following example will illustrate the action of a non-recursive mergesort on a list of 8 values:


5. Merging the two halves of the array in the modified merge function will require the use of a local temporary array. Because the two sublists are stored within one array, the easiest approach is to merge the two sublists into another array, then copy the temp array back to the original.
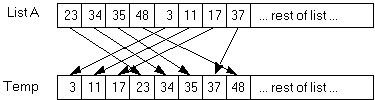
Then copy Temp back into List A:
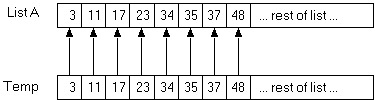
6. This version of merge will need to be able to work with sections of List A. Here is a proposed function prototype for merge:
void merge (apvector<int> &A, int first, int mid, int last);
/* will merge the two sorted sublists within A into one continuous sublist from A[first] .. A[last]. The left list ranges from A[first]..A[mid]. The right list ranges from A[mid+1]..A[last]. */
7. You will need to write the code for this version of function merge to support a recursive mergesort.
C. Recursive Mergesort
1. Instead of dividing the list once, a recursive mergesort will keep dividing the list in half until the sublists are one or two values in length.
2. When
developing a recursive solution, a key step is identifying the base case of the
solution. What situation will
terminate the recursion? In this
case, a sublist of one or two values will be our two base cases.
3. Let's try and work through the recursive mergesort of a list of eight values.
![]()
The list is divided into two sublists.
![]()
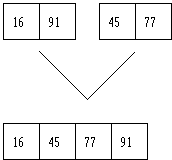
Now let's work on the left sublist. It will be divided into lists of two.
![]()
Each list of two is now very easy to sort. After each list of two is sorted, we then merge these two lists back into a list of four.
Now the algorithm proceeds to solve the right sublist (positions 5-8) recursively. Then the two lists of four are merged back together.
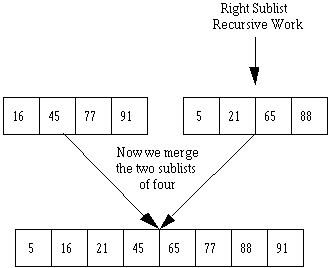
D. Order
of Recursive Mergesort
1. Suppose
we have a list of 8 numbers. If we
trace the migration of one value, it will be a member of the following sizes of
lists: eight, four, two.
The number of calls of mergesort needed to sort one value into its final
resting spot is log2N. If
N = 8, then it will take three calls of the algorithm for one value to find its
final resting spot.
2. We
must apply log2N
steps to N elements in the list. The
order of recursive Mergesort is O(N *
log2N) or O(N *
log N).
3. What about the cost of merging the fragments of the list? The merge algorithm is a linear one, so when combined with the Mergesort routine we have a O (N * log N) + O(N), which remains in the category of an O(N * log N) algorithm.
SUMMARY/REVIEW: When you time and graph the recursive mergesort you will notice a dramatic change in efficiency. This concept of dividing the problem in two is used in several other classic algorithms. Once again, recursion makes it easier to define a problem and code the solution.
ASSIGNMENT: Lab Exercise L.A.22.1, Merge
Lab Exercise LA.22.2, Mergesort (Recursive)