INTRODUCTION:               In Lesson 22, you developed a recursive merge sort algorithm using arrays.  An unordered linked list is difficult to sort given its sequential nature, but a recursive merge sort can be developed for linked lists.  The algorithms required (split and merge) will provide excellent practice in working with linked lists.  After applying a recursive merge sort to a linked list, another function to reverse the list will be written.

The key topics for this lesson are: A.  Merge Sort with Linked Lists        B.   A Reverse List Algorithm 

DISCUSSION:                       A.  Merge Sort with Linked Lists

 1.   A linked list can be sorted using a recursive merge sort algorithm.  Here are the steps:

 a.   Split the list into two smaller lists.

 b.   Recursively sort these two lists using merge sort.

 c.   Merge the two sorted lists together.

 2.   Suppose we begin with a list of seven nodes, pointed to by A.

3.   We then split this list into two smaller lists which differ in size by no more than one node.  It does not matter which values end up in either list.  In the example to follow, list A will take the first half of the list while list B will have the second half of the original list.

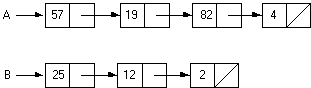
4.   Next, we recursively sort these two lists.

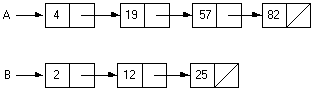
5.   Finally, we merge these two sorted lists together.

6.   The lab exercise gives you more specific instructions about implementing this merge sort concept with linked lists.

B.   A Reverse List Algorithm

 1.   Suppose we take the sorted list from section A.5. above and reverse the order.  The resulting list now looks like this:

2.   In the lab exercise you will develop a function to reverse the order of the nodes in a linked list.  Your algorithm should not create a duplicate list which is reversed in order.  The algorithm should manipulate the nodes of the one list as necessary to produce the reversed list.

SUMMARY/REVIEW:         You are encouraged to look over your code for functions merge and mergesort from Lesson 22.  Reviewing these algorithms as applied to arrays will help you to solve the same mergesort concept with linked lists.

ASSIGNMENT:                    Lab Exercise L.A.34.1, MergeList