Computer
Science - C++
(apmatrix
class)
INTRODUCTION: Two dimensional arrays allow the programmer to solve problems involving rows and columns. Many data processing problems involve rows and columns, such as an airplane reservation system or the mathematical modeling of bacteria growth. A classic problem involving two-dimensional arrays is the bacteria program presented in the lab exercise, Life. After surveying the syntax and unique aspects of these larger data structures, such information will be applied to more challenging lab exercises.
As with the previous lesson, a standard matrix
class will be provided to implement 2-dimensional
arrays. This
apmatrix
class will support routines similar to those used with
the apvector
class.
The key topics for this lesson are:
A. Two-Dimensional Arrays
B. Passing Two-Dimensional Arrays to Functions
C.
Two-Dimensional Array Algorithms
VOCABULARY:
MATRIX
ROW
COLUMN
DISCUSSION:
A. Two-Dimensional Arrays
1.
The apmatrix
class is a two-dimensional version of an array which
uses multiple subscripts. This allows for the creation of
table-like data structures with a row and column
format. The
first subscript will define a row of a table with the
second subscript defining a column of a table.
The apmatrix
class will be used to implement 2-D arrays in the
curriculum guide.
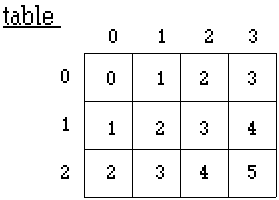
Here is an example program including a diagram
of the array.
Program 18-1
#include <apmatrix.h>
main ()
{
apmatrix<int> table(3,4);
int row, col;
for (row = 0; row <3; row++)
for (col = 0; col <4; col++)
table[row][col] = row + col;
return 0;
}

2.
The declaration of a apmatrix
type is similar to that of an apvector
type. The
data type stored in the apmatrix
is declared between the <type> placeholders.
The size of the table is specified by the
integer arguments inside of the parentheses, i.e.
(3,4).
3.
Just as with one-dimensional arrays, the row and
column numbering of a 2-D array begin at subscript
location zero (0).
The 3 rows of the table are referenced from rows
0..2. Likewise,
the 4 columns of the table are referenced from columns
0..3.
4.
The two-dimensional table
is filled with the sums of row
and col.
To access each location of the matrix, specify
the row coordinate first, then the column:
table
[row][col]
Each subscript must have its own square
brackets. Do
not use table
[row,col] as is used in some other
programming languages such as Pascal
B.
Passing Two-Dimensional Arrays to Functions
1.
The following program will illustrate parameter
passing of an apmatrix.
The purpose of this program is to read a text
file containing integer data, store it in a 2-D array,
and print it out.
The contents of the text file "data.txt"
is shown first:
"data.txt"
17
3 2
13
5
10 11 8
9
6 7
12
4 15 14 1
Program 18-2
#include <apmatrix.h>
#include <iomanip.h>
#include <fstream.h>
#include <iostream.h>
// A program to illustrate apmatrix
parameter passing
const
int MAX =
4;
void printTable (const apmatrix<int> &table);
void
loadTable (apmatrix<int>
&table);
main ()
{
apmatrix<int>
grid(MAX,MAX);
loadTable (grid);
printTable (grid);
return 0;
}
void printTable (const apmatrix<int> &table)
{
for (int row=0; row<MAX; row++)
{
for (int col=0; col<MAX; col++)
cout << setw(4) << table[row][col];
cout << endl;
}
}
void loadTable (apmatrix<int> &table)
{
ifstream inFile("c:\\apcs\\data.txt",ios::in);
for (int col=0; col<MAX; col++)
inFile >> table[row][col];
}
2. The function loadTable uses a reference parameter,
(apmatrix<int> &table).
The local identifier table serves as an alias for the actual
parameter grid
passed to the function.
3. The function printTable uses a const reference parameter,
(const
apmatrix<int>
&table).
This avoids making a local copy of grid,
yet guarding the data of grid
from any changes.
4. The apmatrix class performs range-checking on the indexing operator ([]). If any code attempts to access beyond the boundaries of the matrix, the programs stops.
C. Two-Dimensional Array Algorithms
1.
The most common 2-D array algorithms will
involve processing the entire grid, usually row-by-row
or column-by-column.
2.
Problem-solving on a matrix could involve
processing:
a. one row
b. one column
c. one cell
d.
adjacent cells in various different directions
3. In the next lesson we will look at a 2-D recursive solution to a rather difficult problem.
SUMMARY/REVIEW: Two-dimensional arrays will be applied to two interesting problems. The simulation of life in a petri dish of bacteria will require a two-dimensional array representation. The second and third lab exercises are different versions of the "Knight's Tour" problem, an interesting and demanding chess movement problem.
ASSIGNMENT: Lab Exercise, L.A.18.1, Life
Lab Exercise, L.A.18.2, Knight's Tour 1
Lab
Exercise, L.A.18.3, Knight's
Tour 2