Computer Science - C++ Lesson 36:
Binary Trees
OBJECTIVES:
The student will define the following terms as applied to binary trees: root node, parent node, child node, leaf, levels, edge, and subtree.
The student will draw an ordered binary tree, given a set of data input to the tree.
The student will code a recursive insert algorithm to add data to an ordered binary tree.
The student will describe the best and worst cases for the data set used to construct a binary tree.
INTRODUCTION:
A binary tree is a different kind of data structure which demands new terminology and algorithms. A binary tree node will have two pointers available for linking with other nodes, resulting in diagrams that look like inverted trees. A binary tree will begin with one node at the top and branch out below. As you might expect, the potential of going one of two different ways leads to some challenging programming problems. In fact, the idea of trying one direction, then backtracking must lead to recursion. The recursive algorithms used to traverse binary trees are very elegant and compact, but difficult to understand. But, one step at a time; first we need to learn how to talk about binary trees (vocabulary) and then build one (an algorithm).
The key topics for this lesson are:
A. Binary Tree Vocabulary B. Building a Binary Tree C. Shape of a Binary Tree
VOCABULARY:
| BINARY TREE | LEVELS |
| CHILD NODE | PARENT NODE |
| EDGE | ROOT NODE |
| LEAF | SUBTREE |
DISCUSSION: A. Binary Tree Vocabulary
1. A binary tree is a data structure where each node has two pointers, each pointing to another node or a NULL value.

2. The following binary tree terms will be defined and applied to the above example.
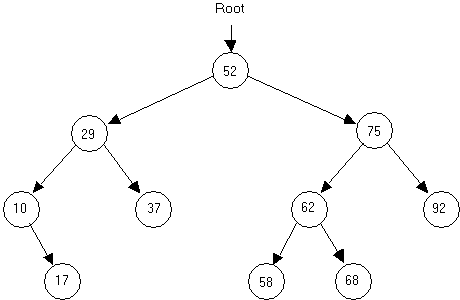
a. Root node - the top node in the tree; the node whose value is 52.
b. Parent node - a node which points to one or two nodes.
c. Child node - the node being pointed to from a parent; every node in the tree is a child to another node, except for the root node.
d. Leaf - a node which has no children
e. Level - the distance from the root, calculated by counting the shortest distance from the root to that node. Examples: 29 is the value stored in a node at level 1, 62 is a value stored in a node at level 2, 17 is the value of a node stored at level 3, etc.
f. Edge - an edge joins two nodes. In the above diagram each arrow represents an edge.
3. This tree is an example of an ordered binary tree which has the following property. For every parent node, a child to the right will have a larger value, while a child to the left will have a smaller value.
4. A subtree is the entire left branch or right branch of a node. For example, the left subtree of the node containing 52 has 4 nodes. The right subtree of node containing 75 has only 1 node.
5. A leaf will have two NULL pointers.
B. Building a Binary Tree
1. The following definitions will apply in this next section on building a binary tree.
struct treeNode
{
int id, inv;
treeNode *left, *right;
treeNode (int, int, treeNode *, treeNode *);
};
treeNode::treeNode (int tempId, int tempInv, treeNode *tempLeft,
treeNode *tempRight)
: id (tempId), inv(tempInv), left(tempLeft), right(tempRight)
{
// all values initialized using initializer list
}
typedef treeNode* treePtr;
2. Suppose the following integers were inserted into a binary tree in this order:
26 79 14 99 53 9 35 21 87
Draw the resulting binary tree:
3. You will notice that new information was placed in the binary tree as a leaf. The insert algorithm will be a recursive solution.
void insert (treePtr &p, int data)
// Will insert data
into an ordered binary tree. The
solution is recursive.
C. Shape of a Binary Tree
1. The shape of a binary tree will affect its performance as a data structure and is dependent on the order of the data set.
2. If the data set came in as a sorted list (1 2 3 4 ...), the binary tree is essentially a linked list with an unused left pointer in each node.
3. A data set in random order will give a more balanced tree.
4. Ideally, we want binary trees that are balanced with almost equal numbers of nodes in each subtree of a node. The characteristic of a balanced binary tree is defined as follows: for every node in the tree, the number of nodes in its left subtree is equal to the number of nodes in its right subtree, plus or minus one. Balancing binary trees will not be covered in this curriculum guide.
SUMMARY/REVIEW: You have learned how to build a binary tree; but is it correct? We need to “see” the tree by printing it out in ascending order. Examine the binary trees developed in this lesson and think about the task of printing out the values in order. The next lesson will introduce you to a recursive solution to this problem, as well as a few other binary tree algorithms.
ASSIGNMENT:
Worksheet W.A.36.1, Binary
Trees
Lab Exercise L.A.36.1, BTree