INTRODUCTION:              

Because a node in a binary tree can have two descendants, deleting such a location can cause a lot of problems.  After examining the code to delete from a binary tree, you will then solve a mirror image variation of this routine in your lab exercise.  The use of diagrams to follow this algorithm is very important.

The key topic for this lesson is:

A.  Deletion from a Binary Tree

B.   Function modifyTree

DISCUSSION:                      

A.  Deletion from a Binary Tree

1.   Deleting a node involves three major steps:

a.   Locating the node to be deleted.

b.   Rerouting pointers to eliminate that node from the data structure.

c.   Disposing of the unwanted memory location.

2.   After locating the node to be deleted, we must determine the nature of that node. 

  a.   If it is a leaf, the rehooking of pointers is simple.

b.   If it has one child, the rehooking of pointers is straight-forward.

c.   If it has two children, the problem becomes much harder to solve.

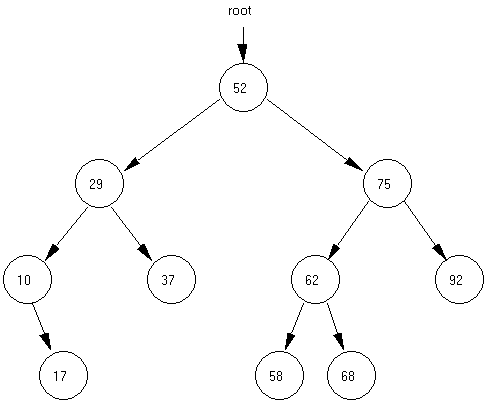
Diagram 38-1

3.   A leaf node containing the value 17 will be easy to delete.  The parent node of the node holding 17 will change its right pointer to NULL and the appropriate memory reclaimed using the C++ delete command.

4.   A node with one child, like the node with value 10, will involve rerouting the node from its parent to its single child.

5.   But rerouting around the node with value 29, a node with two children, involves breaking off subtrees and reattaching them at the proper location. 

7.   The binary tree in Diagram 38-1 has one external pointer (root) and many internal pointers.  Remember that an internal pointer is one which connects one node to another within a dynamic data structure.

8.   After the value to be deleted is input in testDelete, this function calls deleteNode the first time and passes the root pointer to the tree.  The function deleteNode uses an alias (p) as it decides what to do with the pointer it receives.  Function deleteNode has 4 scenarios:

a.   p == NULL, the value does not exist in the tree, return false.

b.   We found the correct node (idToDelete == p->id), call modifyTree and feed it p.

c.   Did not find the node yet, recursively call deleteNode and pass it the internal pointer to the left child, or

d.   Recursively call deleteNode and pass it the internal pointer to the right child.     

9.   It is important to note that except for deleting the root node, the call of modifyTree will be working with p as an alias for an internal pointer. 

B.   Function modifyTree

1.   Working with a smaller version of the same binary tree is Diagram 38-1.  We illustrate the deletion of a leaf node using this diagram.

      Diagram 38-2.

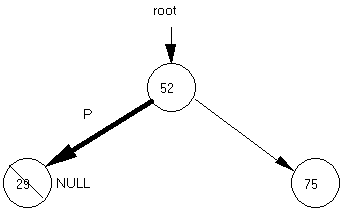
      Suppose we wish to delete the node containing value 29.  The deleteNode function identifies the node to be deleted and sends the internal pointer p to function modifyTree.  Function modifyTree first sets marker = p for the purpose of reclaiming memory at the end of the function.  The function identifies that p is pointing to a leaf node (the first case) and sets p = NULL.  Note that modifyTree receives p as a reference parameter, any change made to p will be reflected back to the calling statement.  Finally, the pointer marker is used to recover memory by calling the C++ delete command.

2.   This relatively easy example of deleting a leaf node illustrates the importance of receiving p as a reference parameter in function modifyTree.  Any changes made to p inside of modifyTree will be permanent changes to an internal pointer inside the tree.

3.   The one-child cases are solved next in modifyTree.  These cases are left for you and your instructor to trace.

4.   The two-child case is more difficult and involves breaking off a branch and re-attaching it to maintain an ordered binary tree.  Suppose in the following diagram we wish to delete the node with value 29.     

      Diagram 38-3.

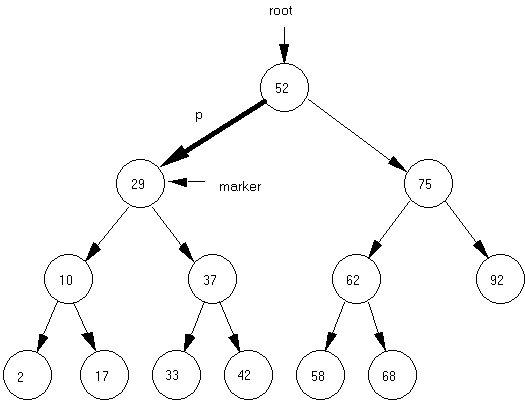
5.   The function deleteNode finds the node to be deleted and calls modifyTree, passing the pointer p as shown in the diagram above.  Here are the steps for deleting a node having two children.

a.   The marker pointer has been already set.

      marker = p;

b.   Re-route p around the node to be deleted.  Pointer p will now point to the left subtree of the deleted node. 

      p = p->left;

c.   Find the correct reattachment point for the right subtree of the deleted node.

        temp = p;

        while (temp->right != NULL)

                temp = temp->right;            // found new attachment point

d.   Reattach the right subtree to maintain an ordered tree.  The right subtree of the deleted node will be attached as the right child of the node containing value 17.

        temp->right = marker->right;

e.   Finally, the node with value 29 is deleted by:

        delete marker;

6.   This entire process for the two-child case could be directed the other way.  Again, suppose the node with value 29 was to be deleted from the original tree.

a.   Pointer p could pick up the right subtree of the node being deleted.

b.   The left subtree of the deleted node is relocated to become the left subtree of the node with value 33.

7.   This approach also successfully deals with deleting the root node.  You should trace the code to confirm that it correctly deals with the root node case.

SUMMARY/REVIEW:         This alternative direction of section B. 6. above will be the basis of your lab exercise.  There are other deletion algorithms, but this one is efficient and clear.  Take some time to review the steps for yourself using the diagrams and code side-by-side.

ASSIGNMENT:                    Lab Exercise L.A.38.1, BTree (Continued)

1.   Copy the functions presented in Handout H.A.38.1, Deletion from a Binary Tree.  However, you are required to solve the 2 child case as a mirror image of the solution described in Section B. 6. of the student outline O.A.38.1 (Page 5).  Change function modifyTree to deal with the two-child case as follows:

a.   The pointer p, which points to the node being deleted, is to be rerouted to the node to the right of the deleted node.

b.   The left subtree of the deleted node is to be moved to the following location:  move one node to the right of the node being deleted, then as far left as possible.

  2.   Test your code and solve the following sequence of run output steps:

a.   Load the file from disk (file20.txt); 

b.   Print the tree.

c.   Print the number of nodes in the tree.

d.   Search for Id values specified by your instructor.  Print out the Id and Inv response in column form.

e    Delete the Id values specified by your instructor.

f.    Print the tree again.

g.   Print the number of nodes in the tree.