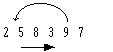
Computer Science - C++ Lesson 20:
quadratic sorting algorithms
INTRODUCTION:
In this lesson, you will learn about three
sorting algorithms:
bubble, selection, and insertion.
After counting the number of steps of each
algorithm, you will have a relative sense of which is
the fastest and the slowest sorting algorithm.
The key topics for this lesson are:
A. Sorting Template Program
B. Bubble Sort
C. Selection Sort
D. Insertion Sort
E. Counting Steps - Quadratic Algorithms
VOCABULARY: BUBBLE SORT SWAP
SELECTION SORT INSERTION SORT
QUADRATIC STUB
NONDECREASING ORDER
DISCUSSION:
A. Sorting Template Program
|
See Handout H.A.20.1, sortTemp.cpp. |
1. A program shell has been provided as Handout H.A.20.1, sortTemp.cpp. |
2.
Examine the sortMenu
function. Notice
the use of character input to process the user choice.
This allows for error-trapping the input if the
value is outside the range 1..6, or if an alphabet
letter is typed in.
3.
The program asks the user to select a sorting
algorithm, fills the array with an amount of data
chosen by the user, calls the sorting algorithm, and
gives an option of printing out the data after it has
been sorted.
4.
In this program the number of data elements
stored in the array is recorded in index position 0.
In function fillArray, the number of data elements in
the vector is stored in temp[0]. The postcondition statement for
function fillArray is that temp
is filled with data from positions 1..n, where n is
stored in temp[0].
5.
At this point, each sorting algorithm has been
left as a function stub.
A stub is an incomplete routine which can be
called but does not solve anything yet.
The stub will be filled in later as each
algorithm is developed and understood.
6.
Stub programming is a programming methodology
strategy used during the implementation stage of
program development.
It allows for the coding and testing of
algorithms in the context of a working program.
As each sorting algorithm is completed, it can
be added to the program shell and tested without having
to complete the other sections.
7. This stepwise development of programs using stub programming will be used extensively in future lessons.
B.
Bubble Sort
1.
Here is a bubble sort algorithm.
void bubbleSort (apvector<int> &list)
{
for (int outer=1; outer <= list[0]-1; outer++)
{
for (int inner=1; inner <= list[0]-outer; inner++)
{
if (list[inner] > list[inner+1])
swap(list[inner], list[inner+1]);
}
}
}
3.
Given an array of 6 values, the loop variables outer
and inner
will evaluate as follows:
When outer = inner ranges from
1 to (6 - outer)
1 1 to 5
2 1 to 4
3 1 to 3
4 1 to 2
5
1 to 1
4.
When outer
= 1, then the inner loop will do 5 comparisons of values
next to each other.
As inner
ranges from 1-5, it does the following comparisons:
inner
if list[inner] > list[inner
+ 1]
1 if list[1] > list[2]
2 if list[2] > list[3]
... ...
5
if list[5] > list[6]
5.
If (list[inner]
> list[inner+1]) is true, then the values are
out of order and a swap takes place.
6.
After the first pass (outer
= 1), the largest value will be in its final resting
place. When
outer = 2,
the inner
loop only goes from 1 to 4 because a comparison between
positions 5 and 6 is unnecessary.
The inner
loop is shrinking.
7.
Because of the presence of duplicate values this
algorithm will result in a list sorted in nondecreasing
order. If
there is a duplicate value it would be incorrect to say
the list is in strictly increasing order because there
will be spots in the list where the values do not
increase.
8.
Here is a small list of data to test your
understanding of Bubble Sort.
Write in the correct sequence of integers after
each advance of outer.
outer
57
95
88
14
25
6
1
_____
_____
_____
_____
_____
_____
2
_____
_____
_____
_____
_____
_____
3
_____
_____
_____
_____
_____
_____
4
_____
_____
_____
_____
_____
_____
5
_____
_____
_____
_____
_____
_____
C. Selection Sort
void selectionSort (apvector<int> &list)
{
int flag;
for (int outer=1; outer < list[0]; outer++)
{
flag = outer;
for (int inner=outer+1; inner<=list[0]; inner++)
{
if (list[inner] < list[flag])
{
flag = inner;
}
}
swap(list[outer], list[flag]);
}
}
2.
Selection sort also uses passes to sort for a
position in the array. Again, assuming we have a list of 6
numbers, the outer
loop will range from 1 to 5.
When outer
= 1, we will look for the smallest value in the list
and move it to the 1st position in the array.
3.
However, when looking for the smallest value to
place in position 1, we will not swap as we search the
entire list. The
algorithm will check from positions 2 to 6, keeping
track of where the smallest value is found by using flag
as a state variable.
After we have found the location of the largest
value in index position flag, we swap list[outer]
and list[flag].
4.
By keeping track of where the smallest value is
located and swapping once, we have a more efficient
algorithm than bubble sort.
5. Here is a small list of numbers to test your understanding of Selection Sort. Fill in the correct numbers for each line after the execution of the outer loop.
outer
57
95
88
14
25
6
1
_____
_____
_____
_____
_____
_____
2
_____
_____
_____
_____
_____
_____
3
_____
_____
_____
_____
_____
_____
4
_____
_____
_____
_____
_____
_____
5
_____
_____
_____
_____
_____
_____
1.
Insertion sort takes advantage of this logic:
If A < B and B < C, then it follows that A
< C. We
can skip the comparison of A and C.
2.
Consider the following partially sorted list of
numbers:
2 5
8 3 9
7
The first three values of the list are sorted.
The 4th value in the list (3), needs to move
back in the list between the 2 and 5.
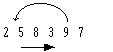
This involves two tasks, finding the correct
insert point and a right shift of any values between
the start and insertion point.
3.
Following is the code:
void
insertionSort
(apvector<int> &list)
{
int outer,
pos, temp;
for (outer=2; outer
<= list[0];
outer++)
{
pos = outer;
temp =
list[pos];
// move list[pos]
out of list
while
((pos > 1) && (list[pos-1]
> temp))
{
list[pos]
= list[pos-1];
pos--;
}
list[pos]
= temp;
}
}
4.
By default, a list of one number is sorted.
Hence the outer
loop skips position 1 and ranges from positions 2 to list[0].
For the sake of discussion, let us assume a list
of 6 numbers.
5.
For each pass of outer,
the algorithm will solve two things concerning the
value stored in list[outer].
It finds the location where list[outer]
needs to be inserted in the list.
Second, it does a right shift on sections of the
array to make room for the inserted value.
6. Constructing the inner while loop is an appropriate place to apply DeMorgan's laws:
a. The inner while loop postcondition has two possibilities:
The value (temp) is larger than its left neighbor.
The value (temp)
moves all the way back to position 1.
b.
This can be summarized as:
(1 == pos
|| list[pos
-1] <= temp)
c.
If we negate the loop postcondition we get the while
loop boundary condition:
(1 != pos
&&
list[pos-1]
> temp)
d.
This can also be rewritten as:
((pos
> 1) && (list[pos-1]
> temp))
7. The two halves of the boundary condition cover these situations:
(list[pos-1]
> temp) -
the value in list[pos-1]
is larger than temp,
keep moving left (pos--) to find the first value
smaller than temp.
8.
This algorithm is appropriate when a list of
data is kept in sorted order with very few changes.
If a new piece of data is added, probably at the
end of the list, it will get inserted back into the
correct position in the list.
All the other values in the list do not move and
the inner while loop will not be used except when
inserting a new value into the list.
9.
Here is the same list of six integers to
practice Insertion Sort.
Outer
57
95
88
14
25
6
2 _____ _____ _____ _____ _____ _____
3 _____ _____ _____ _____ _____ _____
4 _____ _____ _____ _____ _____ _____
5 _____ _____ _____ _____ _____ _____
6 _____ _____ _____ _____ _____ _____
E. Counting Steps - Quadratic Algorithms
1. These three sorting algorithms are categorized as quadratic sorts because the number of steps increases as a quadratic function of the size of the list.
2. It will be very helpful to study algorithms based on the number of steps they require to solve a problem. We will add code to the sorting template program and count the number of steps for each algorithm.
3. This will require the use of a global longint variable - we'll call it steps. We will not pass steps through parameter lists. In this appropriate situation we will use steps as a global counter. You will need to initialize steps to 0 at the appropriate spot in the main menu routine.
4. As you type in the sorting algorithms, add increment statements for the variable steps. For example here are the revised versions of functions swap and bubbleSort:
{
int temp = a;
a = b;
b = temp;
steps += 3;
}
void bubbleSort (apvector<int> &list)
{
steps++; // initialization of outer
for (int outer=1; outer <= list[0]-1; outer++)
{
steps += 3;
// 1 - boundary check of outer loop;
// 2 - increment, outer++
// 3 - initialization of inner loop
for (int inner=1; inner <= list[0]-outer; inner++)
{
steps += 3;
// 1 - boundary check of inner loop
// 2 - increment, inner++
// 3 - if comparison
if (list[inner] > list[inner+1])
{
swap(list[inner], list[inner+1]);
steps++; // call of swap
}
}
}
}
5.
It is helpful to remember that a for
statement is simply a compressed while
statement. Each
for loop has three parts:
initialization, boundary check, and
incrementation.
6.
As you count the number of steps, an interesting
result will show up in your data.
As the size of the data set (n) doubles the
number of steps executed increases at a quadratic rate.
7.
Bubble sort is an example of a quadratic
algorithm in which the number of steps required
increases at a quadratic rate as the size of the data
set increases.
8. A quadratic equation in algebra is one with a squared term, like x2. As the size (n) of the array increases, the number of steps required for any of the quadratic sorts increases by an n2 factor.
SUMMARY/REVIEW: Sorting data by the computer is one of the best applications of computers and software. What takes hours or days by hand can be solved in seconds or minutes by a computer. However, these quadratic algorithms have problems sorting large amounts of data. More efficient sorting algorithms will be covered in later lessons.
ASSIGNMENT:
Lab Exercise L.A.20.1, Quadratics